Qual é a fórmula da área de superfície para uma pirâmide retangular?

A área da superfície será a soma da base retangular e da #4# triângulos, nos quais existem #2# pares de triângulos congruentes.

Área da base retangular

A base simplesmente possui uma área de #lw#, já que é um retângulo.

#=>lw#

Área dos Triângulos Frente e Verso

A área de um triângulo é encontrada através da fórmula #A=1/2("base")("height")#.

Aqui, a base é #l#. Para encontrar a altura do triângulo, devemos encontrar o altura de inclinação naquele lado do triângulo.

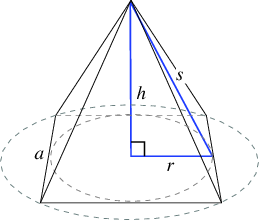
A altura inclinada pode ser encontrada através da resolução da hipotenusa de um triângulo retângulo no interior da pirâmide.

As duas bases do triângulo serão a altura da pirâmide, #h#e metade da largura, #w/2#. Através de teorema de Pitágoras, podemos ver que a altura inclinada é igual a #sqrt(h^2+(w/2)^2)#.

Esta é a altura da face triangular. Assim, a área do triângulo frontal é #1/2lsqrt(h^2+(w/2)^2)#. Como o triângulo traseiro é congruente à frente, sua área combinada é duas vezes a expressão anterior, ou

#=>lsqrt(h^2+(w/2)^2)#

Área dos Triângulos Laterais

A área dos triângulos laterais pode ser encontrada de maneira muito semelhante à dos triângulos anterior e posterior, exceto pelo fato de sua altura inclinada ser #sqrt(h^2+(l/2)^2)#. Assim, a área de um dos triângulos é #1/2wsqrt(h^2+(l/2)^2)# e ambos os triângulos combinados são

#=>wsqrt(h^2+(l/2)^2)#

Superfície total

Basta adicionar todas as áreas das faces.

#"SA"=lw+lsqrt(h^2+(w/2)^2)+wsqrt(h^2+(l/2)^2)#

Esta não é uma fórmula que você deve tentar memorizar. Em vez disso, é um exercício de realmente entender a geometria do prisma triangular (além de um pouco de álgebra).