O que é 'z' para um intervalo de confiança de 88%?

Se procurarmos um intervalo de confiança de 88%, isso significa que queremos apenas uma chance de 12% de que nosso intervalo não contenha o valor verdadeiro. Supondo um teste bilateral, isso significa que queremos uma chance de 6% atribuída a cada cauda do #Z#-distribuição. Assim, buscamos a #z_(alpha//2)# valor de #z_0.06#.

Essa #z# valor em #alpha//2 = 0.06# é a coordenada do #Z#-curva que possui 6% da área da distribuição à direita e, portanto, 94% da área à esquerda. Nós achamos isso #z#-value pela pesquisa inversa em um #z#-tabela.

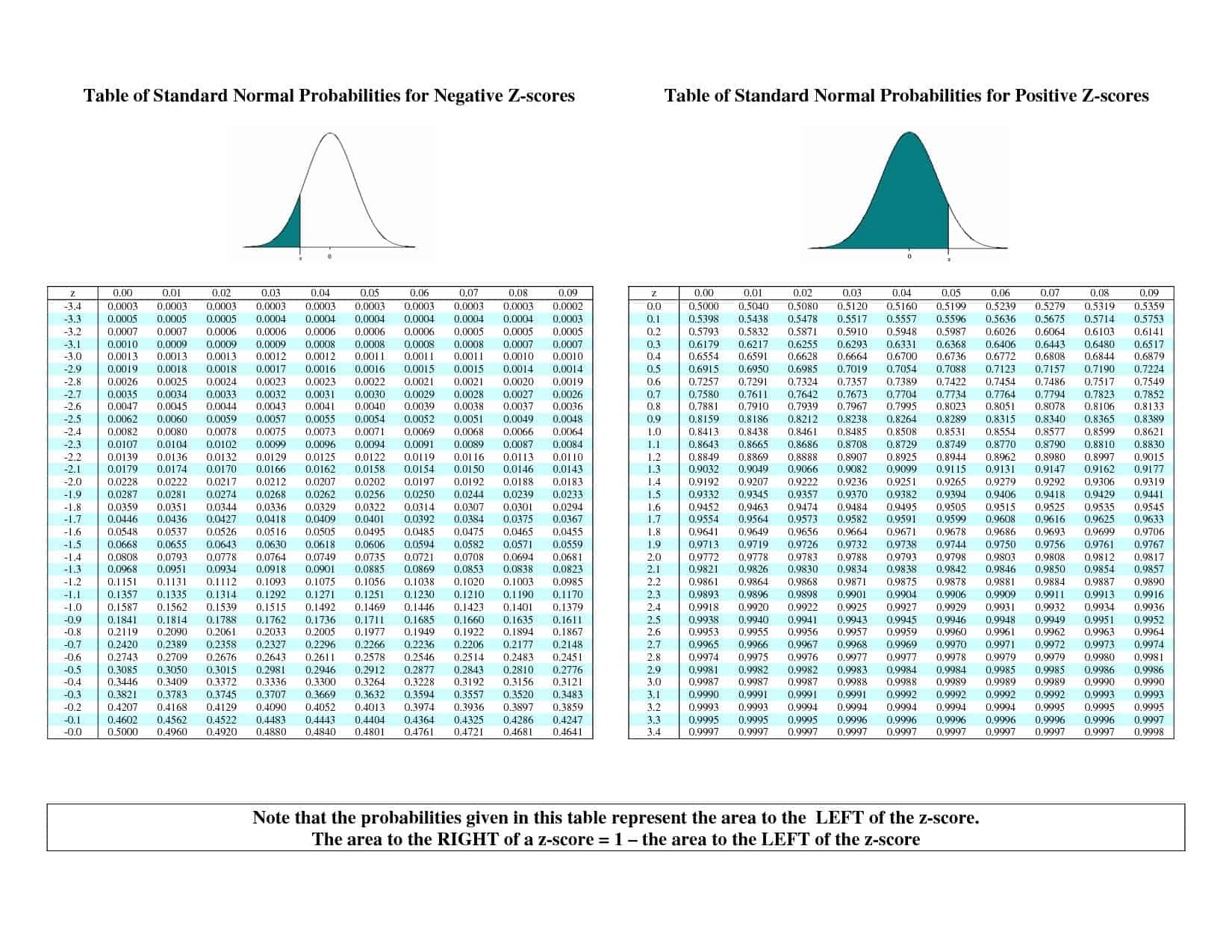
Encontre o valor mais próximo na tabela do 0.9400 possível e veja qual é sua linha e coluna. Pela observação, vemos que o 0.9394 e o 0.9406 estão na tabela com #z#-valores de 1.55 e 1.56, respectivamente, e, para evitar erros, escolheremos o valor que nos oferece um intervalo maior, #z=1.56.#

Observação: Também poderíamos obter uma resposta de software como R, digitando o comando #"qt(0.94, Inf)"#, o que nos daria um valor mais preciso de 1.554774.