Por que um trapézio é um quadrilátero, mas um quadrilátero nem sempre é um trapézio?
Quando você considera o relacionamento entre duas formas, é útil fazê-lo dos dois pontos de vista, ou seja, necessário vs suficiente.
Necessário - #A# não pode existir sem as qualidades de #B#.
Suficiente - As qualidades de #B# descrever suficientemente #A#.
#A# = trapézio
#B# = quadrilátero
Perguntas que você pode querer fazer:
- Um trapézio pode existir sem possuir as qualidades de um quadrilátero?
- As qualidades de um quadrilátero são suficientes para descrever um trapézio?
Bem, a partir dessas perguntas, temos:
- Não. Um trapézio é definido como um quadrilátero com dois lados paralelos. Portanto, a qualidade do "quadrilátero" é necessária, e essa condição é satisfeito.
- Não. Qualquer outra forma pode ter quatro lados, mas se não tiver (pelo menos) dois lados paralelos, não podes ser um trapézio. Um contra-exemplo fácil é um bumerangue, Que possui exatamente quatro lados, mas nenhum deles é paralelo. Portanto, as qualidades de um quadrilátero não descrevem suficientemente um trapézio e essa condição é não satisfeito.
Alguns exemplos malucos de quadriláteros:
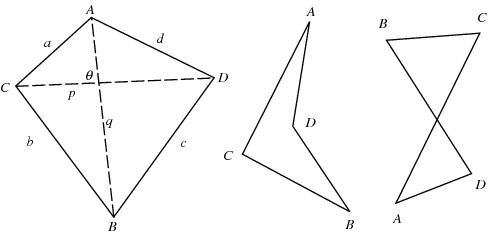
Isso significa que um trapézio é muito específico de um quadrilátero que apenas ter a qualidade de "quadrilátero" não garante a qualidade de "trapézio".
No geral, um trapézio is um quadrilátero, mas um quadrilátero não tem que ser um trapézio.

