Como você determinaria a energia de ionização de um átomo de hidrogênio (em kJ / mol) se o elétron estiver em seu estado fundamental?

Responda:

Vou sugerir duas maneiras de fazer isso.

Explicação:

$color(blue)((1))$

Use a expressão Rydberg:

O comprimento de onda $lambda$ da linha de emissão no espectro de hidrogênio é dada por:

$1/lambda=R[1/n_1^(2)-1/n_2^2]$

$R$ é a constante de Rydberg e tem o valor $1.097xx10^(7)"m"^(-1)$

$n_1$ é o número quântico principal do nível de energia mais baixo

$n_2$ é o número quântico principal do nível de energia mais alto.

Os níveis de energia no hidrogênio convergem e coalescem:

media.web.britannica.com

Desde que o elétron está no $n_1=1$ No estado fundamental, precisamos considerar a série 1. Essas transições ocorrem na parte uv do espectro e são conhecidas como The Lyman Series.

Você pode ver isso como o valor de $n_2$ aumenta então o valor de $1/n_2^2$ diminui. Em valores cada vez mais altos, a expressão tende a zero até que em $n=oo$ podemos considerar que o elétron deixou o átomo resultando em um íon.

A expressão Rydberg agora se torna:

$1/lambda=R[1/n_1^2-0]=R/n_1^2$

Desde $n_1=1$ isso se torna:

$1/lambda=R$

$:.1/lambda=1.097xx10^7$

$:.lambda=9.116xx10^(-8)"m"$

Agora podemos encontrar a frequência e, portanto, a energia correspondente:

$c=nulambda$

$:.nu=c/lambda=(3xx10^(8))/(9.116xx10^-8)=3.291xx10^(15)"s"^(-1)$

Agora podemos usar a expressão Planck:

$E=hnu$

$:.E=6.626xx10^(-34)xx3.291xx10^15=2.18xx10^(-18)"J"$

Essa é a energia necessária para remover o elétron 1 do átomo de hidrogênio 1. Para encontrar a energia necessária para ionizar a mole de átomos H 1, multiplicamos pela constante Avogadro:

$E=2.18xx10^(-18)xx6.02xx10^23=13.123xx10^5"J""/""mol"$

$color(red)(E=1312" ""kJ/mol")$

$color(blue)((2))$

Use o limite de convergência do espectro uv em um método experimental.

Você pode ver no diagrama que os níveis de energia convergem e coalescem em um continuum. Isso significa que as linhas de emissão também convergirão.

A frequência com que isso acontece pode nos dar a energia de ionização.

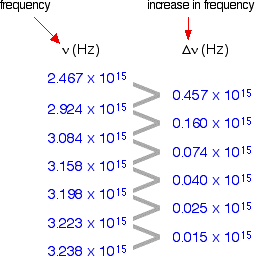
www.chemguide.co.uk

A coluna 1st mostra a frequência da linha.

A segunda coluna mostra a diferença de frequência que está ficando cada vez menos.

Se você planejar $nu$ contra $Deltanu$ você obtém um gráfico como este:

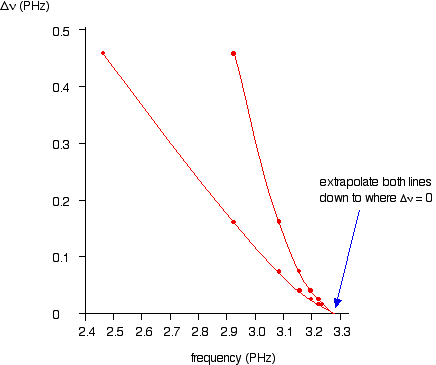
www.chemguide.co.uk

Você pode realmente obter linhas 2 usando valores superiores e inferiores. O ponto importante é que eles convergem para o mesmo ponto em que $Deltanu$ tende a zero.

Você pode ler o limite de convergência fora do eixo x.

Isto dá $nu=3.28xx10^(15)"s"^(-1)$ que é muito próximo do valor do método $color(blue)((1))$ .

Como no método $color(blue)((1))$ podemos converter para Joules usando a expressão Planck:

$E=hnu=6.626xx10^(-34)xx3.28xx10^(15)=2.173xx10^(-18)" ""J"$

Assim, para a toupeira 1:

$E=2.173xx10^(-18)xx6.02xx10^(23)=13.08xx10^(5)"J/mol"$

$color(red)(E=1308" ""kJ/mol")$