Como a velocidade da onda de uma corda é a mesma do cálculo da velocidade usando a cinemática?

Pode ser assim

`v = sqrt(F_T/μ)`

`v = lamdaf" "`esta equação está relacionada à equação anterior

`f = 1/"time required to cover a wavelength"`

`lamda = "wavelength"`

`therefore v = 1/"time required to cover a wavelength" * "wavelength"`

`v = (cancel"(wave)" "length")/("time required to cover" cancel("a wave")"length")`

`therefore v = "length"/"time"`

A velocidade da onda é igual à velocidade da onda, porque as ondas estacionárias se movem apenas em uma direção.

Para entender isso, temos que derivar

`sqrt(F_T/u) = ω/k`

Vamos considerar uma string que tem massa por unidade de comprimento é μ. É esticada por uma tensão T, que é muito maior que o peso da corda e sua posição de equilíbrio é ao longo do eixo x. Este diagrama mostra uma seção curta da corda, esticada na direção x, e as forças que agem sobre ela. Nossa análise se aplica apenas a pequenas deformações, para as quais a corda é um meio linear, e negligenciamos a força gravitacional na corda (que, em qualquer caso, é constante).

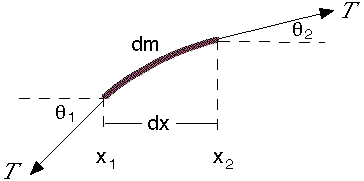
Uma consequência dessa restrição a pequenas deformações é que o ângulo θ entre a corda e a direção x é muito menor que o 1, portanto `sin θ ≅ θ and cos θ ≅ 1`. (No nosso diagrama, no entanto, a deformação foi exagerada para maior clareza.) Segue-se também que o comprimento do segmento mostrado é dx.

Vamos aplicar a segunda lei de Newton na direção vertical y:

`F_y = ma_y`
A soma das forças na direção y é
`F_y = T sin θ2 − T sin θ1.`

Usando a aproximação de ângulo pequeno, sin θ ≅ tan θ = ∂y / ∂x. Então, podemos escrever:

`F_y = T((∂y)/(∂x))_2 - T((∂y)/(∂x))_1`

Portanto, a força total depende da diferença de inclinação entre as duas extremidades: se a corda fosse reta, não importa qual fosse sua inclinação, as duas forças somariam zero. Agora vamos ser quantitativos. A massa por unidade de comprimento é μ, portanto sua massa `dm = μdx`. A aceleração na direção y é a taxa de mudança na velocidade y, então

`a_y = (∂v_y)/(∂t) = ( ∂y^2)/(∂t^2)`.

Então, podemos escrever a segunda lei de Newton na direção y como

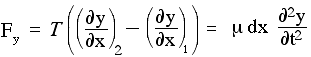
Reorganizar isso dá

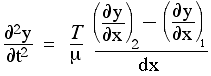
Agora, usamos o subscrito 1 para identificar a posição xe 2 para identificar a posição `(x+dx)`. Portanto, o numerador no último termo à direita é a diferença entre as (primeiras) derivadas nesses dois pontos. Quando a dividimos por `dx`, obtemos a taxa de variação do primeiro derivado em relação a `x`, que é, por definição, a segunda derivada; portanto, derivamos a equação da onda:

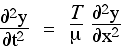
Portanto, a aceleração (à esquerda) é proporcional à tensão T e inversamente proporcional à massa por unidade de comprimento μ. Também é proporcional a `(∂y^2)/(∂x^2)`. Portanto, uma curvatura maior na corda produz uma aceleração maior e, como vimos, uma porção reta não é acelerada. Esta é a equação da onda em uma dimensão. Agora é hora de resolvê-lo.

Uma solução para a equação de onda

Essa é uma equação diferencial parcial. Uma das técnicas mais populares, no entanto, é esta: escolha uma função provável, teste para ver se é uma solução e, se necessário, modifique-a. Então, vamos usar o que já sabemos. Sabemos que as ondas senoidais podem se propagar em um meio unidimensional como uma corda. E sabemos que qualquer função `f(x − vt)` é uma onda que viaja em velocidade v. No primeiro capítulo sobre ondas em movimento, vimos que uma versão elegante da expressão geral para uma onda senoidal que viaja na direção x positiva é`y = A sin (kx − ωt + φ)`. Uma escolha adequada do eixo x ou t nos permite definir φ como zero, então vamos olhar para a equação

`"y" = "A sin"(kx - ωt)`

para ver se e quando esta é uma solução para a onda

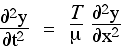
Ao tomar a derivada parcial em relação a t, mantemos x constante e vice-versa. Portanto, lembrando que a derivada de seno é cos e que a derivada de cos é menos seno, podemos escrever as duas primeiras derivadas parciais com relação a t e x assim:

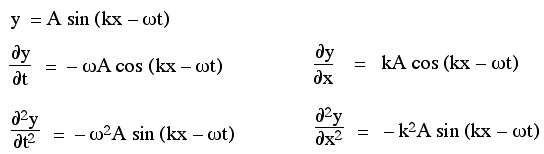
Velocidade da onda em uma corda esticada

Então vimos que as segundas derivadas parciais têm a forma correta, o que significa que estamos no caminho certo. No entanto, para ser uma solução para

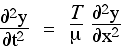
os derivados parciais

`ω/k = sqrt(F_T/μ)`

Para entender de onde vem essa equação, considere uma onda senoidal básica,`A cos (kx−ωt)`. Após o tempo t, a fonte produziu oscilações ωt / 2π = ft`(omega = 2pif)`. Após o mesmo tempo, a frente da onda inicial se propagou para longe da fonte através do espaço até a distância x para se ajustar ao mesmo número de oscilações, kx = ωt.

Assim, a velocidade de propagação v é `v = x/t= ω/k`. A onda se propaga mais rapidamente quando as oscilações de frequência mais alta são distribuídas menos densamente no espaço. [2] Formalmente, `Φ = kx−ωt` é a fase. Desde a `ω = (−dΦ)/(dt)` e `k = (+dΦ)/(dx)`, a velocidade da onda é `v = (dx)/(dt) = ω/k`

E como

`k = 2pie" "e = 1/lamda`

Onde e é a frequência espacial

`k = (2pi)/lamda`

portanto

`w/(2pi)/lamda = f/lamda`