Qual é o componente Z do momento angular orbital? Como podemos encontrar o componente Z? Qual é a sua importância? Com o que isso se parece?
Você parece estar se referindo a #m_l#, que é o valor observado que corresponde à #z#-componente do momento angular total orbital #L_z#.
Na prática, na química geral, você pode simplesmente usar o valor de #l# como o intervalo de #m_l#e expresse #m_l# como:
#bb(m_l = {-l,-l+1, . . . , 0, . . . , l - 1, l})#
Por exemplo, se #l = 2# (como para um #d# orbital), então:
#m_l = {-2,-1,0,+1,+2}#
Isso significa cinco #d# existem orbitais para um determinado número quântico principal #n#:

RELAÇÃO COM O COMPONENTE Z DO MOMENTO ANGULAR ORBITAL TOTAL
Lembre-se de que a equação de Schrodinger é tipicamente escrita como #hatHpsi = Epsi# (Onde #E# é a energia #hatH# é o operador hamiltoniano e #psi# é a função de onda).
Bem, acontece que #psi#, pela função de onda descrevendo o estado de um sistema mecânico quântico, pode ser separado em um radial e um angular componente, #R_(nl)(r)# e #Y_(l)^(m_l)(theta,phi)#:
#psi_(nlm_l)(r,theta,phi) = R_(nl)(r)Y_(l)^(m_l)(theta,phi)#
onde #n#, #l#e #m_l# são o principal, momento angular e magnético Números quânticos, Respectivamente.
Tradicionalmente, #m_l# é definido como o #z# componente do momento angular #l#e é o autovalor (a quantidade que esperamos ver repetidas vezes), em unidades de #ℏ#, da função de onda, #psi#.
Esse valor próprio corresponde ao operador para #L_z#e #L_z# is o #bb(z)# componente do total momento angular orbital.
O que acabamos de dizer pode ser expresso como:
#stackrel("Operator")overbrace(hatL_z)" "stackrel("Angular")stackrel(" Component")stackrel("of Wave Function")overbrace(Y_(l)^(m_l)(theta,phi)) = stackrel("Eigenvalue")overbrace(m_lℏ)" "stackrel("Angular")stackrel(" Component")stackrel("of Wave Function")overbrace(Y_(l)^(m_l)(theta,phi))#
If #L_z# é o que você quer dizer, então o significado disso é que é o fenômeno que podemos observar que corresponde ao número quântico magnético # m_l#.
PERSPECTIVA FÍSICA
Visualmente, na presença de um campo magnético no #z# direção, uma rotação nuclear (exibindo uma momento angular total orbital) ocorre ao longo do #z# chamado de "precessão de Larmor".
Este é o evento descrito por #L_z#.
Por exemplo, quando #l = 1#, como para #p# orbital, #m_l = {-1,0,+1}#. A "precessão Larmor" que ocorre se parece com o seguinte para uma #2p_z# orbital:
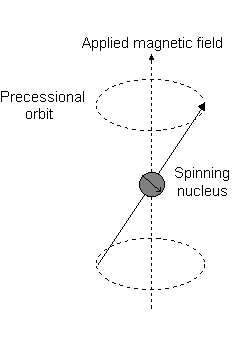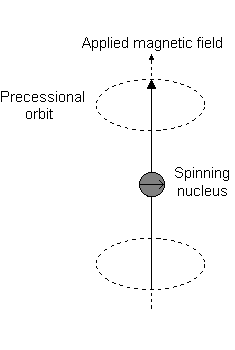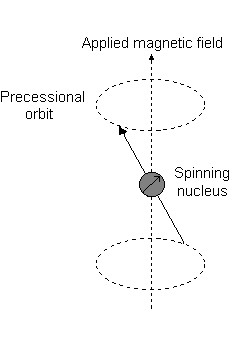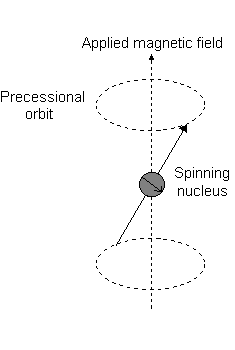
E cada #m_l# corresponde à distância do #z# eixo em unidades de #ℏ#:

Por exemplo:
- An #m_l# of #1# corresponde à metade superior do #2p_z# orbital.
- An #m_l# of #0# é o ponto na origem.
- An #m_l# of #-1# corresponde à metade inferior.
PERSPECTIVA QUÍMICA
Do ponto de vista prático, o que realmente importa é como usar #m_l#. Cada #m_l# corresponde a um orbital único em um subconjunto específico. Tão:
- O número de #m_l# valores informa o número de orbitais em um subshell.
- O alcance de #m_l# é baseado no escolhido #l#.
Por exemplo, desde #l = 2# é para um #d# subshell, então:
#m_l = {-2,-1,0,+1,+2}#
Isso significa cinco #d# existem orbitais para um determinado número quântico principal #n#:


