Como você expressa #cos (pi / 3) * cos ((pi) / 6) # sem usar produtos de funções trigonométricas?
Responda:
A resposta final é #sqrt3/4#
Explicação:
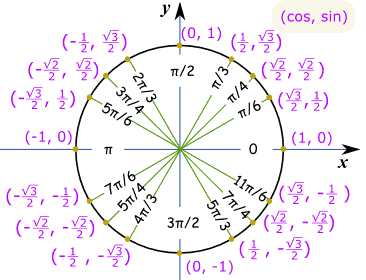
Para funções Trig, aqui está seu melhor amigo, o círculo trigonométrico.
O que você vê aqui é para todas as seções do círculo que você possui; existe um valor para o cosseno e o seno para esse valor.
Portanto, se você olhar para a linha de #pi/3# no primeiro quadrante, o cosseno de #cos(pi/3)#, é igual a #1/2#
Quando você olha para a linha #pi/6# no primeiro quadrante, #cos(pi/6)# é igual a #sqrt3/2#
Então a multiplicação de #cos(pi/3)*cos(pi/6)# é apenas multiplicar frações simples.
#1/2*sqrt3/2=sqrt3/4#

