Como você calcularia a tensão superficial de uma solução 2% (p / v) de um agente umectante que tenha uma densidade de 1.008 g / mL e que aumente 6.6 cm em um tubo capilar com um raio interno de 0.2 mm?

Um método para medir a tensão superficial de um líquido é medir a altura em que o líquido sobe em um tubo capilar.

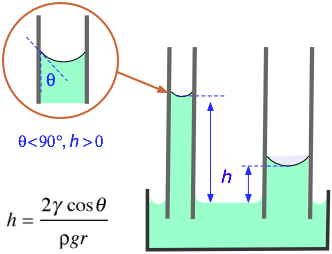
A fórmula é

#color(blue)(|bar(ul(color(white)(a/a) γ = "rhρg"/"2cosθ" color(white)(a/a)|)))" "#

onde

#γ# = tensão superficial
#r# = raio do capilar
#h# = a altura em que o líquido sobe no capilar
#ρ# = o densidade do líquido
#g# = a aceleração devido à gravidade
#θ# = o ângulo de contato com a superfície

Para água pura e vidro limpo, o ângulo de contato é quase zero.

If #θ ≈ 0#, Em seguida #cosθ ≈ 1#, e a equação se reduz a

#color(blue)(|bar(ul(color(white)(a/a) γ = "rhρg"/2 color(white)(a/a)|)))" "#

No seu problema,

#r = "0.2 mm" = 2 × 10^"-4"color(white)(l) "m"#
#h = "6.6 cm" = "0.066 m"#
#ρ = "1.008 g/mL" = "1.008 kg/L" = "1008 kg·m"^"-3"#
#g = "9.81 m·s"^"-2"#

#γ = (2 × 10^"-4" color(red)(cancel(color(black)("m"))) × 0.066 color(red)(cancel(color(black)("m"))) × 1008 color(red)(cancel(color(black)("kg·m"^"-3"))) × 9.81 color(red)(cancel(color(black)("m·s"^"-2"))))/2 × ("1 J")/(1 color(red)(cancel(color(black)("kg")))·"m"^2color(red)(cancel(color(black)("s"^"-2"))))= "0.065 J·m"^"-2" = "65 mJ·m"^"-2" #

Para comparação, a tensão superficial da água pura a 20 ° C é #"73 mJ·m"^"-2"#.